Если оси поверхностей
При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:
1) пересечение поверхностей вращения;
2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;
3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.
Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф1) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П2 или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г2), определены точки видимости С и D линии пересечения относительно плоскости П1. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О1; О2), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах
Rmin < R < Rmах- Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (Rmax = О2В2), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h2) и пересекающей другую (по окружности h3).
Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:
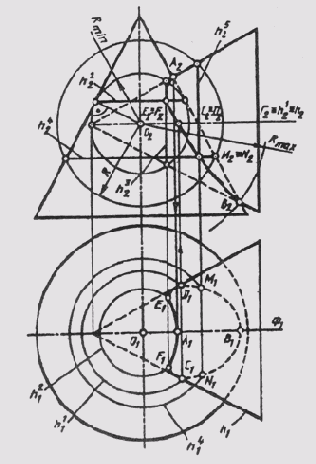
Рис. 135
h22 ^ h32 = E2(F2); Е2Е1 || А2А1;
Е2Е1 ^ h21 =E1; F2F ^ h1 = F1
Промежуточная сфера радиуса R пересекает поверхности по окружностям h4 и h5, в пересечении которых находятся точки Ми N:
h42 ^ h52 = M2(N2); M2M1 || А2А1,
М2М1 ^ h41 = М1; N2N1 ^ h41 = N1
Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.
 |
 |
 |